RSA攻击手法总结
0x00:补充装备
1、网站
factor:http://factordb.com/

还有:https://www.atool99.com/quality_factor.php
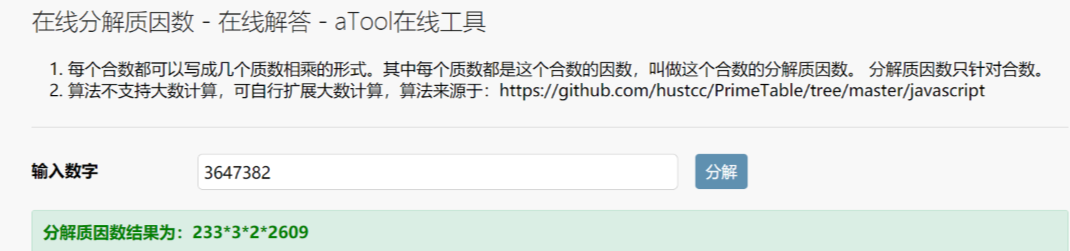
2、工具yafu:
https://sourceforge.net/projects/yafu/
yafu安装之后,可以把该文件夹下程序的路径加入环境变量,方便使用。
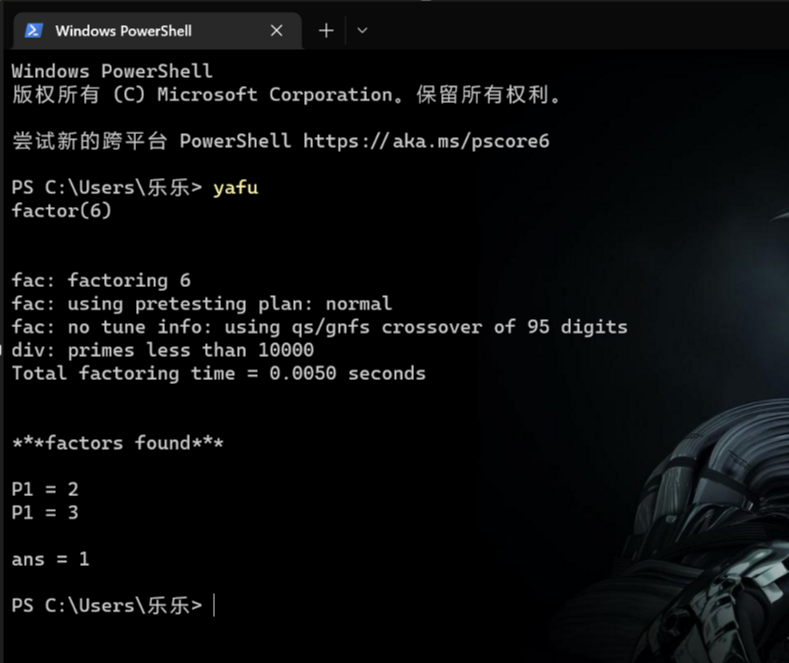
注意,我这里直接用yafu命令就打开了,因为我把yafu-x64.exe重命名为了yafu.exe。
第三方模块gmpy2和libnum的安装教程就不说了,可自行上网搜索。
1、gmpy2
import gmpy2
gmpy2.mpz(n) #初始化一个大整数 n
gmpy2.mpfr(x) #初始化一个高精度浮点数x
d = gmpy2.invert(e,n) #求逆元
c = gmpy2.powmod(m,e,n) #幂取模
gmpy2.is_prime(n) #素数检测
gmpy2.is_even(n) #偶数检测
gmpy2.is_odd(n) #奇数检测
gmpy2.gcd(a,b) #欧几里得算法求最大公约数
gmpy2.gcdext(a,b) #扩展欧几里得算法
gmpy2.iroot(x,n) #x开n次根2、libnum
import libnum
d = libnum.invmod(e,n) #求逆元
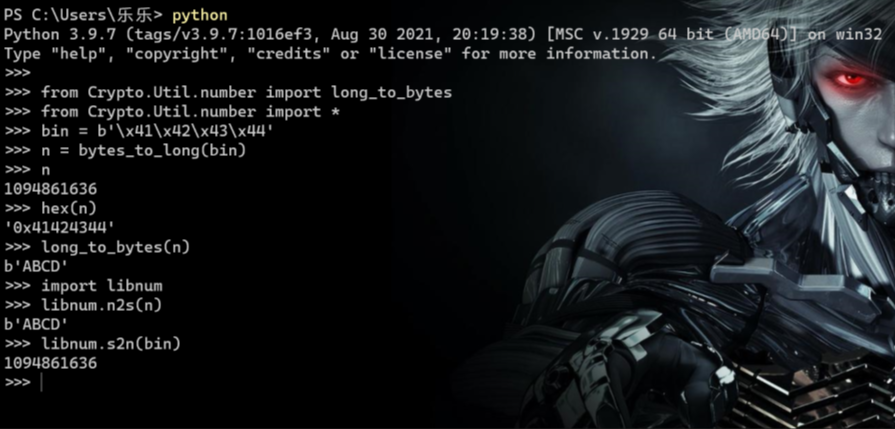
libnum.s2n(str) #字符串按ascii码转换成16进制,16进制再转换成10机制
libnum.n2s(n) #整数转字符串,任意进制数会先转成16进制数
libnum.s2b(str) #字符串转2进制位串
libnum.b2s(bin) #2进制位串转字符串3、Crypto
crypto在python上的名字是pycrypto,是一个第三方模块,目前已经停止更新了。推荐安装pycryptodome是pycrypto的延伸,语法是一样的。
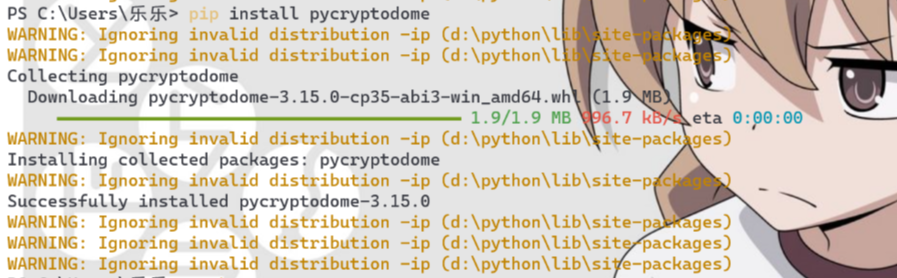
安装完之后有个注意的地方:
Python在引入模块时是对\python\Lib\site-packages这个地方进行查找模块的。在里面有个crypto文件夹,与我们想引入的Crypto名称没对应好。由于大家在引入模块时默认都是Crypto,所以就把文件夹重命名为Crypto。
long_to_bytes和bytes_to_long函数介绍:
0x01:针对RSA的攻击方法
假若$n$较小,以至于在现实意义上能够被分解,那么攻击者就会从而获得私钥$d$:
$$
n=pq\Rightarrow\varphi(n)=(p-1)(q-1)\Rightarrow ed\equiv1\space(mod\space\varphi(n))
$$
得到私钥$d$后可以直接$c^d\equiv m\space(mod\space n)$解密啦~
在团体内部使用RSA加密算法时,有时为了方便而使用相同的模($n$)来进行加解密。此时当使用不同的公钥对同一明文进行加密时,就会存在安全隐患了。
加密过程:$m^{e_1}\equiv c_1\space(mod\space n)$,$m^{e_2}\equiv c_2\space(mod\space n)$.
公钥一般为质数,在不相同时则有:$gcd(e_1,e_2)=1$
进一步有:$k_1e_1+k_2e_2=1,\space k_1,k_2\in Z$ (辗转相除法的逆代可得)
这样就会有:$c_1^{k_1}\times c_2^{k_2}\equiv m\space(mod\space n)$,从而得到明文。
证明:
$\space\space\space\space(c_1^{k_1}\times c_2^{k-2})\space mod \space n$
$=[(c_1\space mod \space n)^{k_1}\times(c_2\space mod \space n)^{k_2}]\space mod\space n$
$=(m^{e_1k_1}\times m^{e_2k_2})\space mod\space n$
$=(m^{k_1e_1+k_2e_2})\space mod\space n$
$=m\space mod \space n$
当RSA系统的公钥$e$选取较小的值时,可以使得加密和验证签名的速度有所提升。但当选取的$e$过小时,就会容易受到低指数攻击。
假设有三个用户的密钥指数为$e$,有不同的模$n_1,n_2,n_3$。一用户对相同的明文$m$使用三个人的公钥加密于三人通话,得到密文$c_1,c_2,c_3$。
$$
m^e\equiv c_1\space(mod\space n_1)
$$
$$
m^e\equiv c_2\space(mod\space n_2)
$$
$$
m^e\equiv c_3\space(mod\space n_3)
$$
三个密文要是被攻击者截获,利用中国剩余定理(一般$n_1,n_2,n_3$互素)即可求解出$m^e$,即使三个模不互素,也可以使用扩展剩余定理来求解。
现RSA系统中,公钥为$(e,n)$,私钥为$(d,n)$。明文为$m$,密文为$c$。公钥是对外开放的,现假定攻击者获取了加密后的密文,如何用选择密文攻击进行破解呢?
攻击者随机找一个随机数$r$,$r<n$。进行如下计算:
- 用公钥对$r$进行加密,得到临时密文$x$:$x=r^e\space mod \space n\space$
- 将临时密文$x$与密文$c$相乘:$y = (x\times c)\space mod \space n\space$
- 求$r$对模$n$的逆元$t$:$tr\equiv 1\space(mod\space n)\space$
由于数字签名的过程也是基于公钥与私钥系统的,当上文中的私钥也用于数字签名时。攻击者只要使对方用私钥$d$对$y$进行签名:$u=y^d\space mod \space n$,然后攻击者得到$u$后,可通过$m=(t\times u)\space mod \space n$解出密文$m$。
推导证明:
$(t\times u)\space mod \space n = (r^{-1}\times y^d)\space mod\space n = (r^{-1}\times x^d \times c^d)\space mod \space n=c^d\space mod\space n=m$
0x02:例题实战
https://www.ctf.show/challenges#easyrsa1-344
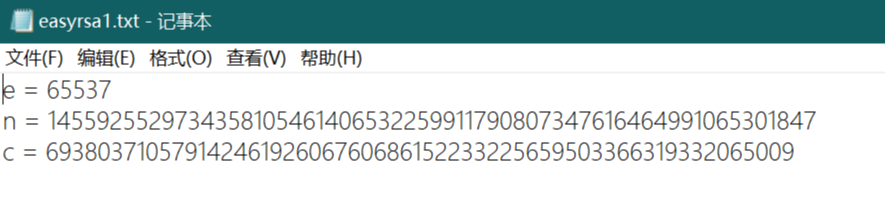
由于$n$较小,所以直接用第一种攻击手法,即分解$n$,从而得到$d$来解密。
质因数分解:
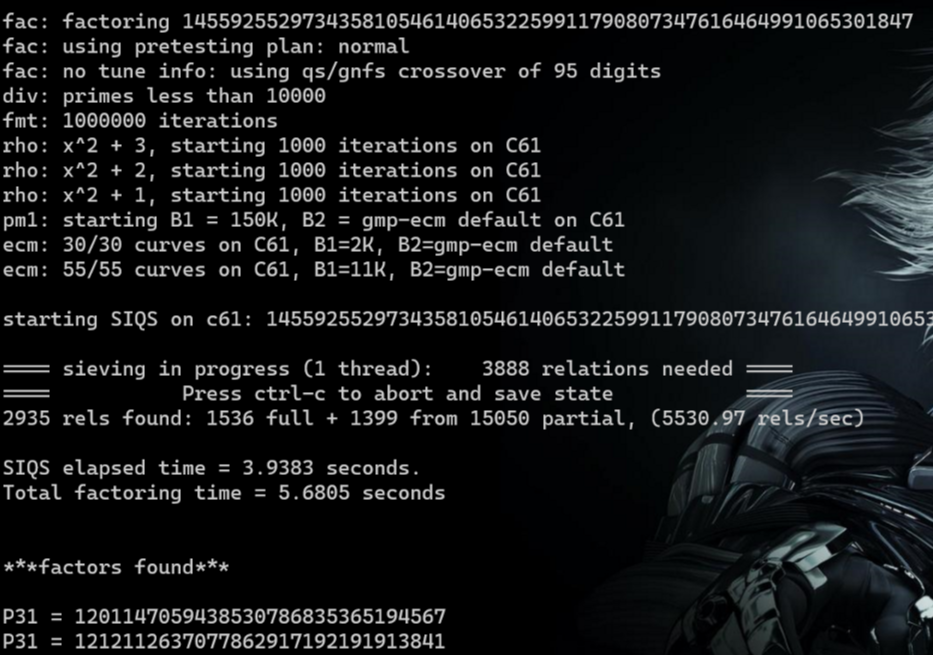
p = 1201147059438530786835365194567
q = 1212112637077862917192191913841
脚本:
import libnum
from Crypto.Util.number import long_to_bytes
e = 65537
n = 1455925529734358105461406532259911790807347616464991065301847
c = 69380371057914246192606760686152233225659503366319332065009
p = 1201147059438530786835365194567
q = 1212112637077862917192191913841
phi = (p-1)*(q-1)
d = libnum.invmod(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))https://www.ctf.show/challenges#easyrsa3-346
打开文件分现模$n$是相同的,这里加密的明文应该是flag,所以可以猜测是同一个明文加密。可以采用公共模攻击,具体的证明上面已给出。
脚本:
import gmpy2
from Crypto.Util.number import long_to_bytes
e1 = 797
n = 15944475431088053285580229796309956066521520107276817969079550919586650535459242543036143360865780730044733026945488511390818947440767542658956272380389388112372084760689777141392370253850735307578445988289714647332867935525010482197724228457592150184979819463711753058569520651205113690397003146105972408452854948512223702957303406577348717348753106868356995616116867724764276234391678899662774272419841876652126127684683752880568407605083606688884120054963974930757275913447908185712204577194274834368323239143008887554264746068337709465319106886618643849961551092377843184067217615903229068010117272834602469293571
c1 = 11157593264920825445770016357141996124368529899750745256684450189070288181107423044846165593218013465053839661401595417236657920874113839974471883493099846397002721270590059414981101686668721548330630468951353910564696445509556956955232059386625725883038103399028010566732074011325543650672982884236951904410141077728929261477083689095161596979213961494716637502980358298944316636829309169794324394742285175377601826473276006795072518510850734941703194417926566446980262512429590253643561098275852970461913026108090608491507300365391639081555316166526932233787566053827355349022396563769697278239577184503627244170930
e2 = 521
n = 15944475431088053285580229796309956066521520107276817969079550919586650535459242543036143360865780730044733026945488511390818947440767542658956272380389388112372084760689777141392370253850735307578445988289714647332867935525010482197724228457592150184979819463711753058569520651205113690397003146105972408452854948512223702957303406577348717348753106868356995616116867724764276234391678899662774272419841876652126127684683752880568407605083606688884120054963974930757275913447908185712204577194274834368323239143008887554264746068337709465319106886618643849961551092377843184067217615903229068010117272834602469293571
c2 = 6699274351853330023117840396450375948797682409595670560999898826038378040157859939888021861338431350172193961054314487476965030228381372659733197551597730394275360811462401853988404006922710039053586471244376282019487691307865741621991977539073601368892834227191286663809236586729196876277005838495318639365575638989137572792843310915220039476722684554553337116930323671829220528562573169295901496437858327730504992799753724465760161805820723578087668737581704682158991028502143744445435775458296907671407184921683317371216729214056381292474141668027801600327187443375858394577015394108813273774641427184411887546849
k = gmpy2.gcdext(e1,e2)
m1 = gmpy2.powmod(c1,k[1],n)
m2 = gmpy2.powmod(c2,k[2],n)
m = (m1*m2) % n
print(long_to_bytes(m))https://www.ctf.show/challenges#easyrsa4-347
该题的$e$特别小,可以采用低加密指数攻击。
因为$e$特别小,有两种情况:
- $m^3 < n$,则$c = m^3$
- $m^3 > n$, 则$c = (m^3 + i\times n)\space mod\space n$ (使用爆破)
这里先试着对$c$开$3$次根,发现开出来是个整数(True),然后打印一下。
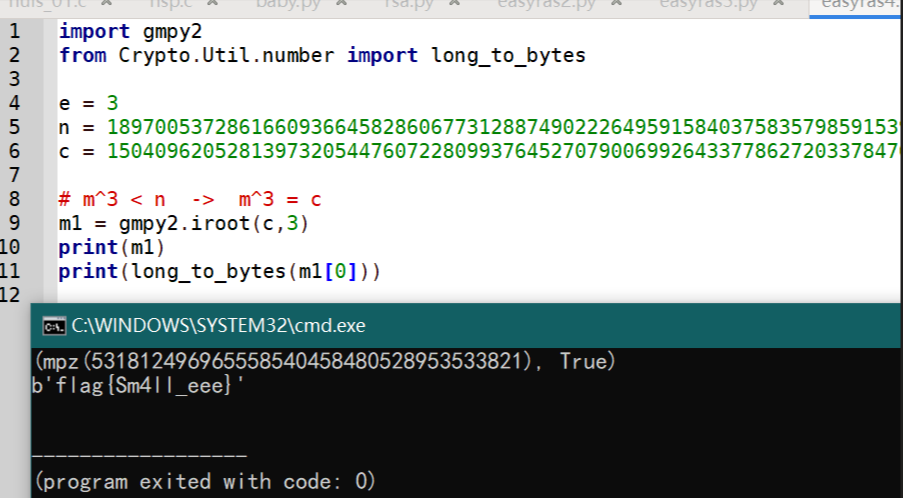
上面的是低加密指数攻击,这道题$e$特别大,比$n$还大,说明$d$会比较小。所以,可以采用低解密指数攻击。详细的攻击手法可参考:
这里直接用大佬的脚本:
https://github.com/pablocelayes/rsa-wiener-attack
这里要把涉及到的py文件下下载到同一的文件夹下。我github不太会用,一个个复制粘贴:(
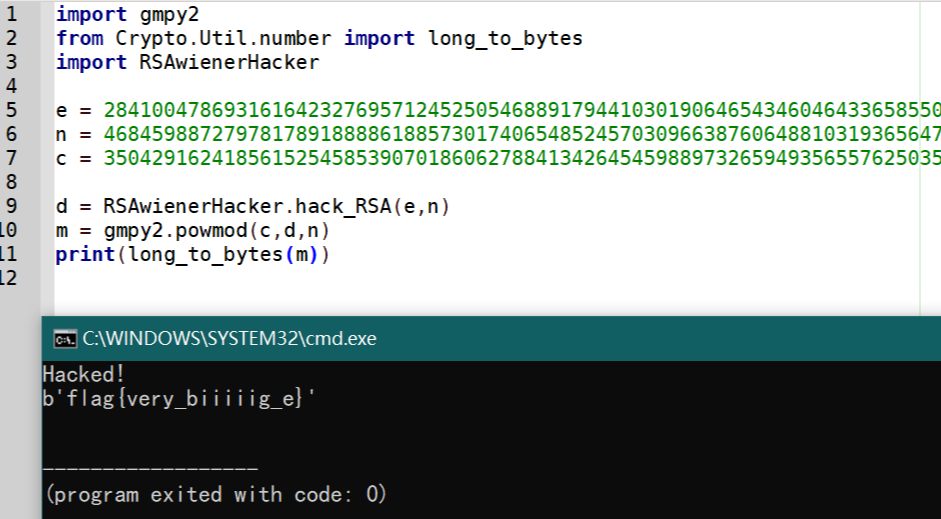
↶ 返回首页